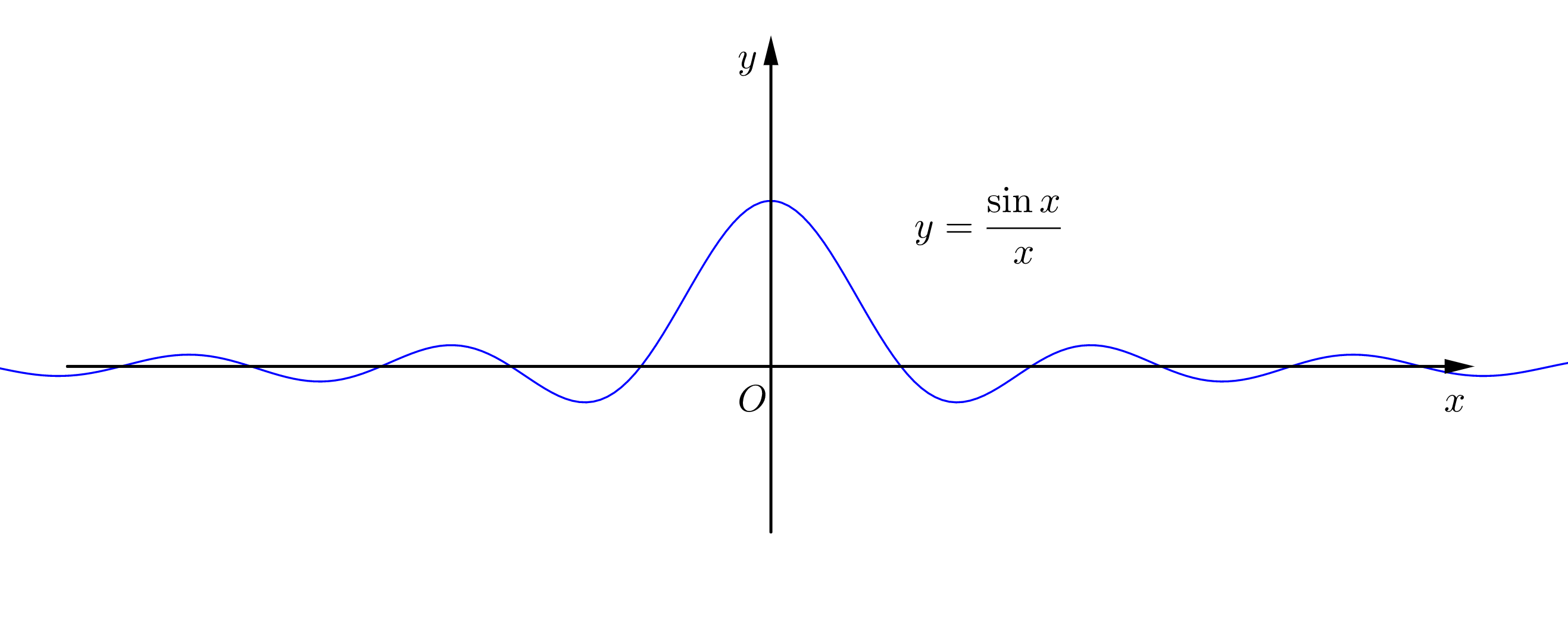
狄利克雷积分   ∫ 0 ∞ sin ⁡ x x d x   \,\displaystyle \int_{0}^{\infin}\frac{\sin x}{x}dx\, ∫0∞​xsinx​dx 是一个比较常见的无穷积分，在很多领域有着重要应用。

  下面介绍几种巧妙解法。为了您更好的阅读体验，请使用电脑浏览。

∫ 0 ∞ sin ⁡ x x d x = lim ⁡ m → ∞ ∫ 0 m π sin ⁡ x x d x \int_{0}^{\infin}\frac{\sin x}{x}dx=\lim_{m\to\infin}\int_0^{m\pi}\frac{\sin x}{x}dx ∫0∞​xsinx​dx=m→∞lim​∫0mπ​xsinx​dx 令   h = π / k ，将区间   [ 0 , m π ]   分割成   k m   个长度为   h   的小区间，由黎曼积分的定义 \text{令}\,h=\pi/k\text{，将区间}\,[0,m\pi]\,\text{分割成}\,km\,\text{个长度为}\,h\,\text{的小区间，由黎曼积分的定义} 令h=π/k，将区间[0,mπ]分割成km个长度为h的小区间，由黎曼积分的定义 ∫ 0 m π sin ⁡ x x d x = lim ⁡ h → 0 + ∑ n = 1 k m sin ⁡ n h n h h = lim ⁡ h → 0 + ∑ n = 1 k m sin ⁡ n h n \int_0^{m\pi}\frac{\sin x}{x}dx=\lim_{h\to0^+}\sum_{n=1}^{km}\frac{\sin nh}{nh}h=\lim_{h\to0^+}\sum_{n=1}^{km}\frac{\sin nh}{n} ∫0mπ​xsinx​dx=h→0+lim​n=1∑km​nhsinnh​h=h→0+lim​n=1∑km​nsinnh​ 由   Fourier   正弦展开 \text{由}\,\textrm{Fourier}\,\text{正弦展开} 由Fourier正弦展开 π − h 2 = ∑ n = 1 ∞ sin ⁡ n h n , ( 0 < h < π ) \frac{\pi-h}{2}=\sum_{n=1}^{\infin}\frac{\sin nh}{n},(0 0 ，对   f ( t )   作拉普拉斯变换，令 \begin{aligned}\text{令}\,f(t)=\int_{0}^{\infin}\frac{\sin tx}{x}\,dx,\, t>0\text{，对}\,f(t)\, \text{作拉普拉斯变换，令}\end{aligned} 令f(t)=∫0∞​xsintx​dx,t>0，对f(t)作拉普拉斯变换，令​ F ( s ) = L [ f ( t ) ] = L [ ∫ 0 ∞ sin ⁡ t x x d x ] t = ∫ 0 ∞ 1 x L [ sin ⁡ t x ] t d x = ∫ 0 ∞ 1 s 2 + x 2   d x = 1 s ∫ 0 ∞ 1 1 + ( x s ) 2   d ( x s ) ( let   u   =   x s ) = 1 s arctan ⁡ u   ∣ 0 ∞ = 1 s π 2 \begin{aligned}F(s)=\mathscr{L}[f(t)]&=\mathscr{L}\Big[\int_{0}^{\infin}\frac{\sin tx}{x}dx\Big]_t\\&=\int_{0}^{\infin} \frac{1}{x}\mathscr{L}\big[\sin tx \big]_tdx\\&=\int_{0}^{\infin}\frac{1}{s^2+x^2}\,dx\\&=\frac{1}{s}\int_{0}^{\infin}\frac{1}{1+(\displaystyle \frac{x}{s})^2}\,d(\frac{x}{s}) \quad (\textit{let u = $\displaystyle \frac{x}{s}$})\\&=\frac{1}{s}\arctan u\,\Big|_0^{\infin}\\&=\frac{1}{s}\frac{\pi}{2}\end{aligned} F(s)=L[f(t)]​=L[∫0∞​xsintx​dx]t​=∫0∞​x1​L[sintx]t​dx=∫0∞​s2+x21​dx=s1​∫0∞​1+(sx​)21​d(sx​)(let u = sx​)=s1​arctanu∣∣∣​0∞​=s1​2π​​ 则    f ( t ) = L − 1 [ F ( s ) ] = π 2 L − 1 [ 1 s ] = π 2 . \begin{aligned}\text{则}\,\, f(t)=\mathscr{L}^{-1}\big[F(s)\big]=\frac{\pi}{2}\mathscr{L}^{-1}\big[\frac{1}{s}\big]=\frac{\pi}{2}\end{aligned}. 则f(t)=L−1[F(s)]=2π​L−1[s1​]=2π​​.

令人惊奇的是， f ( t )   的值竟与   t   无关，于是我们得到一个更为普遍的结论 \begin{aligned}\text{令人惊奇的是，}f(t)\, \text{的值竟与} \,t\, \text{无关，于是我们得到一个更为普遍的结论}\end{aligned} 令人惊奇的是，f(t)的值竟与t无关，于是我们得到一个更为普遍的结论​ ∫ 0 ∞ sin ⁡ t x x   d x = π 2 ,   t > 0 \int_0^{\infin}\frac{\sin tx}{x}\,dx=\frac{\pi}{2},\,t>0 ∫0∞​xsintx​dx=2π​,t>0 如果你也觉得不可思议的话，不妨看看我的解释 \text{如果你也觉得不可思议的话，不妨看看我的解释} 如果你也觉得不可思议的话，不妨看看我的解释 f ′ ( t ) = ∫ 0 ∞ ∂ ∂ t ( sin ⁡ t x x ) d x = ∫ 0 ∞ cos ⁡ t x   d x = lim ⁡ n → ∞ ∫ 0 n π / t cos ⁡ t x   d x ( l e t    u = t x ) = lim ⁡ n → ∞ 1 t ∫ 0 n π cos ⁡ u   d u = 1 t lim ⁡ n → ∞ sin ⁡ u   ∣ 0 n π = 0 \begin{aligned}f'(t)&=\int_0^{\infin}\frac{\partial }{\partial t}\Big(\frac{\sin tx}{x}\Big)dx \\&=\int_0^{\infin}\cos tx\,dx\\&=\lim_{n\to\infin}\int_0^{n\pi/t}\cos tx\,dx \quad (let\,\, u=tx)\\&=\lim_{n\to\infin}\frac{1}{t}\int_0^{n\pi}\cos u\,du\\&=\frac{1}{t}\lim_{n\to\infin} \sin u\,\Big|_0^{n\pi}\\&=0\end{aligned} f′(t)​=∫0∞​∂t∂​(xsintx​)dx=∫0∞​costxdx=n→∞lim​∫0nπ/t​costxdx(letu=tx)=n→∞lim​t1​∫0nπ​cosudu=t1​n→∞lim​sinu∣∣∣​0nπ​=0​ 所以   f ( t ) = C ,   与   t   无关 . \text{所以}\,f(t)=C,\,\text{与}\,t\,\text{无关}. 所以f(t)=C,与t无关.

令 \text{令} 令 f ( t ) = { 1 ,    ∣ t ∣ < 1 0 ,    ∣ t ∣ ≥ 1 f(t)=\begin{cases}1,\,\,|t|∞,0,​t=0t​=0​，且满足∫−∞∞​δ(t)dt=1.

容易验证： ∫ − ∞ ∞ δ ( t ) f ( t ) d t = f ( 0 ) . \text{容易验证：}\displaystyle\int_{-\infin}^{\infin}\delta(t)f(t)dt=f(0). 容易验证：∫−∞∞​δ(t)f(t)dt=f(0).

取   f ( t ) = e − i μ t ,   f ( 0 ) = 1. \text{取}\,f(t)=e^{-i\mu t},\,f(0)=1. 取f(t)=e−iμt,f(0)=1.

则脉冲函数的傅里叶变换    F ( μ ) = F [ δ ( t ) ] = ∫ − ∞ ∞ δ ( t ) e − i μ t d t = 1 \text{则脉冲函数的傅里叶变换}\,\,\displaystyle F(\mu)=\mathscr{F}[\delta(t)]=\int_{-\infin}^{\infin} \delta(t)e^{-i\mu t}dt=1 则脉冲函数的傅里叶变换F(μ)=F[δ(t)]=∫−∞∞​δ(t)e−iμtdt=1.

作傅里叶反变换    δ ( t ) = F − 1 [ F ( μ ) ] = 1 2 π ∫ − ∞ ∞ e i μ t d μ . \text{作傅里叶反变换}\,\,\displaystyle\delta(t)=\mathscr{F}^{-1}\big[F(\mu)\big]=\frac{1}{2\pi}\int_{-\infin}^{\infin} e^{i\mu t}d\mu. 作傅里叶反变换δ(t)=F−1[F(μ)]=2π1​∫−∞∞​eiμtdμ.

准备工作完成，构造函数 \text{准备工作完成，构造函数} 准备工作完成，构造函数   g ( λ ) = ∫ − ∞ ∞ sin ⁡ λ x x d x ，则   g ( 1 ) = ∫ − ∞ ∞ sin ⁡ x x d x . \,\displaystyle g(\lambda)=\int_{-\infin}^{\infin}\frac{\sin \lambda x}{x}dx\text{，则}\,g(1)=\int_{-\infin}^{\infin}\frac{\sin x}{x}dx. g(λ)=∫−∞∞​xsinλx​dx，则g(1)=∫−∞∞​xsinx​dx.

g ′ ( λ ) = ∫ − ∞ ∞ ∂ ∂ λ ( sin ⁡ λ x x ) d x = ∫ − ∞ ∞ cos ⁡ λ x d x + 0 = ∫ − ∞ ∞ cos ⁡ λ x d x + i ∫ − ∞ ∞ sin ⁡ λ x d x = ∫ − ∞ ∞ e i λ x d x = 2 π ( 1 2 π ∫ − ∞ ∞ e i λ x d x ) = 2 π δ ( λ ) \begin{aligned}g'(\lambda)&=\int_{-\infin}^{\infin}\frac{\partial }{\partial \lambda}\Big( \frac{\sin \lambda x}{x}\Big)dx\\&=\int_{-\infin}^{\infin}\cos \lambda xdx+0\\&=\int_{-\infin}^{\infin}\cos \lambda x dx+i\int_{-\infin}^{\infin}\sin \lambda x dx\\&=\int_{-\infin}^{\infin}e^{i\lambda x}dx\\&=2\pi \big(\frac{1}{2\pi}\int_{-\infin}^{\infin}e^{i\lambda x}dx\big)\\&=2\pi \delta(\lambda)\end{aligned} g′(λ)​=∫−∞∞​∂λ∂​(xsinλx​)dx=∫−∞∞​cosλxdx+0=∫−∞∞​cosλxdx+i∫−∞∞​sinλxdx=∫−∞∞​eiλxdx=2π(2π1​∫−∞∞​eiλxdx)=2πδ(λ)​

因为   g ( λ )   是奇函数，所以 \text{因为}\,g(\lambda)\,\text{是奇函数，所以} 因为g(λ)是奇函数，所以

g ( 1 ) = − g ( − 1 ) = 1 2 (   g ( 1 ) − g ( − 1 )   ) ( 由   N - L   公式 ) = 1 2 ∫ − 1 1 g ′ ( λ ) d λ = 1 2 ∫ − 1 1 2 π δ ( λ ) d λ      ( δ ( λ ) = 0 ,   λ ≠ 0 ) = π ∫ − ∞ ∞ δ ( λ ) d λ = π \begin{aligned}g(1)&=-g(-1)\\&=\frac{1}{2}\big(\,g(1)-g(-1)\,\big) \quad (\text{由}\, N\text{-}L\, \text{公式})\\&=\frac{1}{2} \int_{-1}^{1}g'(\lambda)d\lambda\\&=\frac{1}{2} \int_{-1}^{1} 2\pi \delta(\lambda) d\lambda \quad\,\,\,\, (\delta(\lambda)=0,\,\lambda\neq0)\\&=\pi \int_{-\infin}^{\infin}\delta(\lambda)d\lambda\\&=\pi\end{aligned} g(1)​=−g(−1)=21​(g(1)−g(−1))(由N-L公式)=21​∫−11​g′(λ)dλ=21​∫−11​2πδ(λ)dλ(δ(λ)=0,λ​=0)=π∫−∞∞​δ(λ)dλ=π​ 妙极！ \text{妙极！} 妙极！

定理内容：当被积函数   f ( x )   是   x   的有理函数(多项式除多项式)，且分母的次数比分子 \begin{aligned}\text{定理内容：当被积函数} \,f(x)\, \text{是}\, x \,\text{的有理函数(多项式除多项式)，且分母的次数比分子}\end{aligned} 定理内容：当被积函数f(x)是x的有理函数(多项式除多项式)，且分母的次数比分子​ 的次数至少高一次， f ( z )   在实轴上除去有限多个一级奇点   x 1 , x 2 , ⋯   , x p   外处处解析， \begin{aligned}\text{的次数至少高一次，}f(z)\,\text{在实轴上除去有限多个一级奇点}\,x_1,x_2,\cdots,x_p\, \text{外处处解析，}\end{aligned} 的次数至少高一次，f(z)在实轴上除去有限多个一级奇点x1​,x2​,⋯,xp​外处处解析，​ 在上半复平面   ( I m   z > 0 )   除去有限多个奇点   z 1 , z 2 , ⋯   , z q   外处处解析，则 \begin{aligned}\text{在上半复平面}\,(\mathrm{Im}\,z>0)\,\text{除去有限多个奇点}\,z_1,z_2,\cdots,z_q\,\text{外处处解析，则}\end{aligned} 在上半复平面(Imz>0)除去有限多个奇点z1​,z2​,⋯,zq​外处处解析，则​

∫ − ∞ ∞ f ( x ) e i m x d x = π i ∑ k = 1 p R e s [ f ( z ) e i m z , x k ] + 2 π i ∑ k = 1 q R e s [ f ( z ) e i m z , z k ] \int_{-\infin}^{\infin}f(x)e^{imx}dx=\pi i\sum_{k=1}^{p}\mathrm{Res}[f(z)e^{imz},x_k]+2\pi i\sum_{k=1}^{q}\mathrm{Res}[f(z)e^{imz},z_k] ∫−∞∞​f(x)eimxdx=πik=1∑p​Res[f(z)eimz,xk​]+2πik=1∑q​Res[f(z)eimz,zk​]

其中   R e s [ f ( z ) , z 0 ]   为函数   f   在   z 0   处的留数，定义如下： \begin{aligned}\text{其中}\,\mathrm{Res}[f(z),z_0]\,\text{为函数}\,f\,\text{在}\,z_0\,\text{处的留数，定义如下：}\end{aligned} 其中Res[f(z),z0​]为函数f在z0​处的留数，定义如下：​

   若   z 0   是   f ( z )   的孤立奇点， f ( z )   在   D = { z   ∣   0 < ∣ z − z 0 ∣ < R }   内解析， C   是   D   内包 \begin{aligned}&\text{若}\,z_0\,\text{是}\,f(z)\,\text{的孤立奇点，}f(z)\,\text{在}\,D=\{z\,|\,0